BONS ESTUDOS.... RIBAMAR FILHO

Introdução
Conjuntos são um dos conceitos básicos da matemática. Um conjunto é apenas uma coleção de entidades, chamadas de elementos. A notação padrão lista os elementos separados por vírgulas entre chaves (o uso de "parênteses" ou "colchetes" é incomum) como os seguintes exemplos:
- {1, 2, 3}
- {1, 2, 2, 1, 3, 2}
- {x : x é um número inteiro tal que 0
<4}
Os três exemplos acima são maneiras diferentes de representar o mesmo conjunto.
É possível descrever o mesmo conjunto de diferentes maneiras: listando os seus elementos (ideal para conjuntos pequenos e finitos) ou definindo uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell).
Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.
União, interseção e diferença
A união (ou reunião) de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem ao menos a um dos conjuntos
composto dos elementos que pertencem ao menos a um dos conjuntos  e
e  .
.
A união de N conjuntos  é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos
é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos 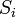 .
.
A interseção de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem simultaneamente aos dois conjuntos
composto dos elementos que pertencem simultaneamente aos dois conjuntos  e
e  .
.
A diferença entre dois conjuntos  e
e  é o conjunto de todos os elementos de
é o conjunto de todos os elementos de  que não pertencem a
que não pertencem a  .
.
Notação dos conjuntos
Os conjuntos são representados de diversas formas:
- A forma mais usual é a que apresenta os elementos entre duas chaves ({});
- As propriedades ou descrições de um conjunto são representadas dentro das {}, após os elementos e separadas destes por :;
- Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
Exemplos de conjuntos compostos por números
Nota: Nesta seção, a, b e c são números naturais, enquanto r e s são números reais.
- Números naturais são usados para contar. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números inteiros aparecem como soluções de equações como x + a = b. O símbolo
 usualmente representa este conjunto (do termo alemão Zahlen que significa números).
usualmente representa este conjunto (do termo alemão Zahlen que significa números). - Números racionais aparecem como soluções de equações como a + bx = c. O símbolo
 usualmente representa este conjunto (da palavra quociente).
usualmente representa este conjunto (da palavra quociente). - Números algébricos aparecem como soluções de equações polinomiais (com coeficientes inteiros) e envolvem raízes e alguns outros números irracionais. O símbolo
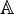 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. - Números reais incluem os números algébricos e os números transcendentais. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto.
Intervalo (matemática)
Origem: Wikipédia, a enciclopédia livre.
Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos. Os extremos podem ser números reais como podem ser 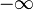 e
e  .
.
Representação
Uma maneira de representar os intervalos, mais comum é a seguinte:
Notação em símbolos de um intervalo
Habitualmente se utilizam os colchetes - “[” e “]” - para indicar que um dos extremos do intervalo é parte deste intervalo e os parênteses - “(” e “)” - ou, também, os colchetes invertidos - “]” e “[” para indicar o contrário.
Assim, por exemplo, dados a e b números reais, com a ≤ b, o intervalo I = (a,b] = ]a,b] representa o conjunto dos x ε R, tal que a < style="font-weight: bold;">a não faz parte do intervalo.
Representação de um intervalo na reta real
Um intervalo é representado na reta real utilizando-se de uma pequena “bolinha vazia” para indicar que um dos pontos extremos não pertence ao intervalo e de uma “bolinha cheia” para indicar que o ponto extremo pertence.
Tipos de Intervalos
Dados a e b números reais, com a ≤ b, x pertencente ao intervalo e c o seu comprimento, podemos classificar os intervalos como:
a) Intervalo Fechado de comprimento finito c = b - a:
[a,b] = {x ε R | a ≤ x ≤ b}
b) Intervalo fechado à esquerda e aberto à direita de comprimento finito c = b - a:
[a,b[ = [a,b) = {x ε R | a ≤ x <>
c) Intervalo aberto à esquerda e fechado à direita de comprimento finito c = b - a:
(a,b] = ]a,b] = {x ε R | a <>
d) Intervalo aberto de comprimento finito c = b - a:
]a,b[ = (a,b) = {x ε R | a <>
e) Intervalo aberto à direita de comprimento infinito:
]-∞,b[ = (-∞,b) = {x ε R | x <>
f) Intervalo fechado à direita de comprimento infinito:
]-∞,b] = (-∞,b] = {x ε R | x ≤ b}
g) Intervalo fechado à esquerda de comprimento infinito:
[a,+∞) = [a,+∞[ = {x ε R | a ≤ x}
h) Intervalo aberto à esquerda de comprimento infinito:
]a,+∞[ = (a,+∞) = {x ε R | x > a}
i) Intervalo aberto de comprimento infinito:
]-∞,+∞[ = (-∞,+∞) = R
j) Intervalo fechado de comprimento nulo:
Como o comprimento é nulo e o intervalo fechado, então a = b e esse intervalo corresponde ao conjunto unitário {a}, isto é, a um ponto da reta real.
Concluo a classificação dos intervalos com a seguinte pergunta para vocês: E o intervalo vazio como seria definido?
União e Intersecção de Intervalos
Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
Sejam A = [-1,6] = {x ε R | -1 ≤ x ≤ 6} e B = (1,+∞) = {x ε R | x > 1} dois intervalos e vamos determinar A U B e A ∩ B.
Primeiramente, marcamos todos os pontos que são extremos ou origens dos intervalos em uma mesma reta. Em seguida, abaixo dessa reta, traçamos os intervalos que representam graficamente os conjuntos A e B. E, por fim, é só utilizar a definição de união e intersecção para determinar os trechos que estão em pelo menos um intervalo e os trechos comuns aos dois intervalos, respectivamente. Veja a solução de A ∩ B na figura a seguir e de onde é também facilmente observado o resultado de A U B:
A ∩ B = {x ε R | 1 < b =" {x">
Questões:
1) Qual a importância do Diagrama de Venn-Euler para os conjuntos?
2) Defina o conjunto dos números reais.
3) Qual a importância do estudo do intervalo para solução de conjuntos ?
4) o símbolo +∞ representa o que ?
5) Leia por extensão :
S = {____________________}
![]a,b[ = (a,b) = \{x\in\mathbb{R}: a<x<b\}\,](http://upload.wikimedia.org/math/a/c/a/acaf312a89ea337af3239f9dfdf95714.png)

![]a,b] = (a,b] = \{x\in\mathbb{R}: a<x\leq b\}\,](http://upload.wikimedia.org/math/8/d/7/8d774f6c464d9d5a82de8dd0b224e147.png)
![[a,b] = [a,b] = \{x\in\mathbb{R}: a\leq x\leq b\}\,](http://upload.wikimedia.org/math/3/f/9/3f9596d211122bb8684d5803df792b79.png)
