INICIANDO O ANO DE 2009 EM NOSSO LABORATÓRIO DE INFORMÁTICA INTRODUZIMOS O CONTEÚDO JA ESTUDADO SOBRE CONJUNTOS PARA DESENVOLVERMOS E SEGUIRMOS NOSSO PROJETO ....
BONS ESTUDOS.... RIBAMAR FILHO

Introdução
Conjuntos são um dos conceitos básicos da matemática. Um conjunto é apenas uma coleção de entidades, chamadas de elementos. A notação padrão lista os elementos separados por vírgulas entre chaves (o uso de "parênteses" ou "colchetes" é incomum) como os seguintes exemplos:
- {1, 2, 3}
- {1, 2, 2, 1, 3, 2}
- {x : x é um número inteiro tal que 0<4}
Os três exemplos acima são maneiras diferentes de representar o mesmo conjunto.
É possível descrever o mesmo conjunto de diferentes maneiras: listando os seus elementos (ideal para conjuntos pequenos e finitos) ou definindo uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell).
Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.
União, interseção e diferença
-
 Ver artigo principal: União
Ver artigo principal: União
A união (ou reunião) de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem ao menos a um dos conjuntos
composto dos elementos que pertencem ao menos a um dos conjuntos  e
e  .
.
A união de N conjuntos  é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos
é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos 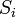 .
.
-
A interseção de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem simultaneamente aos dois conjuntos
composto dos elementos que pertencem simultaneamente aos dois conjuntos  e
e  .
.
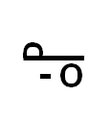
A diferença entre dois conjuntos  e
e  é o conjunto de todos os elementos de
é o conjunto de todos os elementos de  que não pertencem a
que não pertencem a  .
.
Notação dos conjuntos
Os conjuntos são representados de diversas formas:
- A forma mais usual é a que apresenta os elementos entre duas chaves ({});
- As propriedades ou descrições de um conjunto são representadas dentro das {}, após os elementos e separadas destes por :;
- Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
Exemplos de conjuntos compostos por números
Nota: Nesta seção, a, b e c são números naturais, enquanto r e s são números reais.
- Números naturais são usados para contar. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números inteiros aparecem como soluções de equações como x + a = b. O símbolo
 usualmente representa este conjunto (do termo alemão Zahlen que significa números).
usualmente representa este conjunto (do termo alemão Zahlen que significa números). - Números racionais aparecem como soluções de equações como a + bx = c. O símbolo
 usualmente representa este conjunto (da palavra quociente).
usualmente representa este conjunto (da palavra quociente). - Números algébricos aparecem como soluções de equações polinomiais (com coeficientes inteiros) e envolvem raízes e alguns outros números irracionais. O símbolo
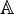 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. - Números reais incluem os números algébricos e os números transcendentais. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto.
Intervalo (matemática)
Origem: Wikipédia, a enciclopédia livre.
Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos. Os extremos podem ser números reais como podem ser 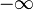 e
e  .
.
Representação
Uma maneira de representar os intervalos, mais comum é a seguinte:
Notação em símbolos de um intervalo
Habitualmente se utilizam os colchetes - “[” e “]” - para indicar que um dos extremos do intervalo é parte deste intervalo e os parênteses - “(” e “)” - ou, também, os colchetes invertidos - “]” e “[” para indicar o contrário.
Assim, por exemplo, dados a e b números reais, com a ≤ b, o intervalo I = (a,b] = ]a,b] representa o conjunto dos x ε R, tal que a < style="font-weight: bold;">a não faz parte do intervalo.
Representação de um intervalo na reta real
Um intervalo é representado na reta real utilizando-se de uma pequena “bolinha vazia” para indicar que um dos pontos extremos não pertence ao intervalo e de uma “bolinha cheia” para indicar que o ponto extremo pertence.

Tipos de Intervalos
Dados a e b números reais, com a ≤ b, x pertencente ao intervalo e c o seu comprimento, podemos classificar os intervalos como:
a) Intervalo Fechado de comprimento finito c = b - a:
[a,b] = {x ε R | a ≤ x ≤ b}
b) Intervalo fechado à esquerda e aberto à direita de comprimento finito c = b - a:
[a,b[ = [a,b) = {x ε R | a ≤ x <>
c) Intervalo aberto à esquerda e fechado à direita de comprimento finito c = b - a:
(a,b] = ]a,b] = {x ε R | a <>
d) Intervalo aberto de comprimento finito c = b - a:
]a,b[ = (a,b) = {x ε R | a <>
e) Intervalo aberto à direita de comprimento infinito:
]-∞,b[ = (-∞,b) = {x ε R | x <>
f) Intervalo fechado à direita de comprimento infinito:
]-∞,b] = (-∞,b] = {x ε R | x ≤ b}
g) Intervalo fechado à esquerda de comprimento infinito:
[a,+∞) = [a,+∞[ = {x ε R | a ≤ x}
h) Intervalo aberto à esquerda de comprimento infinito:
]a,+∞[ = (a,+∞) = {x ε R | x > a}
i) Intervalo aberto de comprimento infinito:
]-∞,+∞[ = (-∞,+∞) = R
j) Intervalo fechado de comprimento nulo:
Como o comprimento é nulo e o intervalo fechado, então a = b e esse intervalo corresponde ao conjunto unitário {a}, isto é, a um ponto da reta real.
Concluo a classificação dos intervalos com a seguinte pergunta para vocês: E o intervalo vazio como seria definido?
União e Intersecção de Intervalos
Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
Sejam A = [-1,6] = {x ε R | -1 ≤ x ≤ 6} e B = (1,+∞) = {x ε R | x > 1} dois intervalos e vamos determinar A U B e A ∩ B.
Primeiramente, marcamos todos os pontos que são extremos ou origens dos intervalos em uma mesma reta. Em seguida, abaixo dessa reta, traçamos os intervalos que representam graficamente os conjuntos A e B. E, por fim, é só utilizar a definição de união e intersecção para determinar os trechos que estão em pelo menos um intervalo e os trechos comuns aos dois intervalos, respectivamente. Veja a solução de A ∩ B na figura a seguir e de onde é também facilmente observado o resultado de A U B:
A ∩ B = {x ε R | 1 < b =" {x">

Questões:
1) Qual a importância do Diagrama de Venn-Euler para os conjuntos?
2) Defina o conjunto dos números reais.
3) Qual a importância do estudo do intervalo para solução de conjuntos ?
4) o símbolo +∞ representa o que ?
5) Leia por extensão :

S = {____________________}







grandezas.jpg)






 e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem ao menos a um dos conjuntos
composto dos elementos que pertencem ao menos a um dos conjuntos  é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos
é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos 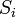 .
. composto dos elementos que pertencem simultaneamente aos dois conjuntos
composto dos elementos que pertencem simultaneamente aos dois conjuntos  usualmente representa este conjunto.
usualmente representa este conjunto. usualmente representa este conjunto (do termo alemão Zahlen que significa números).
usualmente representa este conjunto (do termo alemão Zahlen que significa números). usualmente representa este conjunto (da palavra quociente).
usualmente representa este conjunto (da palavra quociente).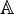 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. usualmente representa este conjunto.
usualmente representa este conjunto.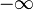 e
e  .
.![]a,b[ = (a,b) = \{x\in\mathbb{R}: a<x<b\}\,](http://upload.wikimedia.org/math/a/c/a/acaf312a89ea337af3239f9dfdf95714.png)

![]a,b] = (a,b] = \{x\in\mathbb{R}: a<x\leq b\}\,](http://upload.wikimedia.org/math/8/d/7/8d774f6c464d9d5a82de8dd0b224e147.png)
![[a,b] = [a,b] = \{x\in\mathbb{R}: a\leq x\leq b\}\,](http://upload.wikimedia.org/math/3/f/9/3f9596d211122bb8684d5803df792b79.png)
