BONS ESTUDOS.... RIBAMAR FILHO

Introdução
Conjuntos são um dos conceitos básicos da matemática. Um conjunto é apenas uma coleção de entidades, chamadas de elementos. A notação padrão lista os elementos separados por vírgulas entre chaves (o uso de "parênteses" ou "colchetes" é incomum) como os seguintes exemplos:
- {1, 2, 3}
- {1, 2, 2, 1, 3, 2}
- {x : x é um número inteiro tal que 0
<4}
Os três exemplos acima são maneiras diferentes de representar o mesmo conjunto.
É possível descrever o mesmo conjunto de diferentes maneiras: listando os seus elementos (ideal para conjuntos pequenos e finitos) ou definindo uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell).
Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.
União, interseção e diferença
A união (ou reunião) de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem ao menos a um dos conjuntos
composto dos elementos que pertencem ao menos a um dos conjuntos  e
e  .
.
A união de N conjuntos  é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos
é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos 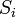 .
.
A interseção de dois conjuntos  e
e  é o conjunto
é o conjunto  composto dos elementos que pertencem simultaneamente aos dois conjuntos
composto dos elementos que pertencem simultaneamente aos dois conjuntos  e
e  .
.
A diferença entre dois conjuntos  e
e  é o conjunto de todos os elementos de
é o conjunto de todos os elementos de  que não pertencem a
que não pertencem a  .
.
Notação dos conjuntos
Os conjuntos são representados de diversas formas:
- A forma mais usual é a que apresenta os elementos entre duas chaves ({});
- As propriedades ou descrições de um conjunto são representadas dentro das {}, após os elementos e separadas destes por :;
- Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
Exemplos de conjuntos compostos por números
Nota: Nesta seção, a, b e c são números naturais, enquanto r e s são números reais.
- Números naturais são usados para contar. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números inteiros aparecem como soluções de equações como x + a = b. O símbolo
 usualmente representa este conjunto (do termo alemão Zahlen que significa números).
usualmente representa este conjunto (do termo alemão Zahlen que significa números). - Números racionais aparecem como soluções de equações como a + bx = c. O símbolo
 usualmente representa este conjunto (da palavra quociente).
usualmente representa este conjunto (da palavra quociente). - Números algébricos aparecem como soluções de equações polinomiais (com coeficientes inteiros) e envolvem raízes e alguns outros números irracionais. O símbolo
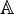 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. - Números reais incluem os números algébricos e os números transcendentais. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto.
Intervalo (matemática)
Origem: Wikipédia, a enciclopédia livre.
Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos. Os extremos podem ser números reais como podem ser 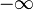 e
e  .
.
Representação
Uma maneira de representar os intervalos, mais comum é a seguinte:
Notação em símbolos de um intervalo
Habitualmente se utilizam os colchetes - “[” e “]” - para indicar que um dos extremos do intervalo é parte deste intervalo e os parênteses - “(” e “)” - ou, também, os colchetes invertidos - “]” e “[” para indicar o contrário.
Assim, por exemplo, dados a e b números reais, com a ≤ b, o intervalo I = (a,b] = ]a,b] representa o conjunto dos x ε R, tal que a < style="font-weight: bold;">a não faz parte do intervalo.
Representação de um intervalo na reta real
Um intervalo é representado na reta real utilizando-se de uma pequena “bolinha vazia” para indicar que um dos pontos extremos não pertence ao intervalo e de uma “bolinha cheia” para indicar que o ponto extremo pertence.
Tipos de Intervalos
Dados a e b números reais, com a ≤ b, x pertencente ao intervalo e c o seu comprimento, podemos classificar os intervalos como:
a) Intervalo Fechado de comprimento finito c = b - a:
[a,b] = {x ε R | a ≤ x ≤ b}
b) Intervalo fechado à esquerda e aberto à direita de comprimento finito c = b - a:
[a,b[ = [a,b) = {x ε R | a ≤ x <>
c) Intervalo aberto à esquerda e fechado à direita de comprimento finito c = b - a:
(a,b] = ]a,b] = {x ε R | a <>
d) Intervalo aberto de comprimento finito c = b - a:
]a,b[ = (a,b) = {x ε R | a <>
e) Intervalo aberto à direita de comprimento infinito:
]-∞,b[ = (-∞,b) = {x ε R | x <>
f) Intervalo fechado à direita de comprimento infinito:
]-∞,b] = (-∞,b] = {x ε R | x ≤ b}
g) Intervalo fechado à esquerda de comprimento infinito:
[a,+∞) = [a,+∞[ = {x ε R | a ≤ x}
h) Intervalo aberto à esquerda de comprimento infinito:
]a,+∞[ = (a,+∞) = {x ε R | x > a}
i) Intervalo aberto de comprimento infinito:
]-∞,+∞[ = (-∞,+∞) = R
j) Intervalo fechado de comprimento nulo:
Como o comprimento é nulo e o intervalo fechado, então a = b e esse intervalo corresponde ao conjunto unitário {a}, isto é, a um ponto da reta real.
Concluo a classificação dos intervalos com a seguinte pergunta para vocês: E o intervalo vazio como seria definido?
União e Intersecção de Intervalos
Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
Sejam A = [-1,6] = {x ε R | -1 ≤ x ≤ 6} e B = (1,+∞) = {x ε R | x > 1} dois intervalos e vamos determinar A U B e A ∩ B.
Primeiramente, marcamos todos os pontos que são extremos ou origens dos intervalos em uma mesma reta. Em seguida, abaixo dessa reta, traçamos os intervalos que representam graficamente os conjuntos A e B. E, por fim, é só utilizar a definição de união e intersecção para determinar os trechos que estão em pelo menos um intervalo e os trechos comuns aos dois intervalos, respectivamente. Veja a solução de A ∩ B na figura a seguir e de onde é também facilmente observado o resultado de A U B:
A ∩ B = {x ε R | 1 < b =" {x">
Questões:
1) Qual a importância do Diagrama de Venn-Euler para os conjuntos?
2) Defina o conjunto dos números reais.
3) Qual a importância do estudo do intervalo para solução de conjuntos ?
4) o símbolo +∞ representa o que ?
5) Leia por extensão :
S = {____________________}
![]a,b[ = (a,b) = \{x\in\mathbb{R}: a<x<b\}\,](http://upload.wikimedia.org/math/a/c/a/acaf312a89ea337af3239f9dfdf95714.png)

![]a,b] = (a,b] = \{x\in\mathbb{R}: a<x\leq b\}\,](http://upload.wikimedia.org/math/8/d/7/8d774f6c464d9d5a82de8dd0b224e147.png)
![[a,b] = [a,b] = \{x\in\mathbb{R}: a\leq x\leq b\}\,](http://upload.wikimedia.org/math/3/f/9/3f9596d211122bb8684d5803df792b79.png)

64 comentários:
Respostas
1º)É a representação gráfica dos conjuntos, através de entidades geométricas.
2º)Números reais incluem os números algébricos e os números transcendentais. O símbolo R usualmente representa este conjunto.
3º)Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos.
4º)Comprimento infinito.
5º)S = {XER|A < X < B} P.S: menor ou igual a B.
Grupo: Henrique Mendes
Jayan Duarte
Caio Jasminie
Francisco Yago
Pedro Felipe
1° A
equipe :
Handressa Silva
Maria Gislayne
Thinayra Jamile
respostas:
1- O Diagrama de Venn-Euler é importante porque é a representação gráfica dos conjuntos, através de entidades geométricas.
2- Os números reais incluem os números algébricos e os números transcendentais; ou seja, é a união de todos os conjuntos.
3- O intervalo são os subconjuntos do conjunto real que forma desigualdade; ou seja, números entre um e outro.
4- Infinito
5- S={ x ε R | a < x ≤ b }
lê-se : x pertence ao conjunto dos números reais tal que x menor que a e x maior ou igual que b.
1° A
equipe:
Handressa Silva
Maria Gislayne
Thinayra Jamile
1- O Diagrama de Venn-Euler é importante porque é a representação gráfica dos conjuntos, através de entidades geométricas
2- Os números reais incluem os números algébricos e os números transcendentais; ou seja, é a união de todos os conjuntos.
3- O intervalo são os subconjuntos do conjunto dos números reais que forma desigualdade, ou seja, número entre um e outro.
4- Infinito
5- S= { x ε R | a < x ≤ b}
lê-se : x pertence ao conjunto dos números reais tal que x menor que a e maior ou igual a b.
Escola:Polivalente
Alunas:Aparecida Patricia
Priscila Macêdo
Gabriele Brito
Série:1 ano ''a'' Turno: manhã
Respostas :
1- É importante para a representação gráfica dos conjuntos, através de entidades geométricas.
2-O conjunto dos números reais é uma expansão do conjunto dos números racionais que engloba não só inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
3-Para poder representar os conjuntos, e para que possamos identificar e entender com mais clareza.
4-Representa infinito positivo.
5- S={xEr|a < X = b }
Escola de ensino fundamental e médio Presidente Geisel (Polivalente)
1º ano
Equipe: José Anderson
Alisson Ribeiro
Respostas:
1ª)Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
2ª)Números reais incluem os números algébricos e os números transcendentais. O símbolo {R} usualmente representa este conjunto.
3ª)E a maneira mais fácil e intuitiva de realizar essas operações é através da representação gráfica dos intervalos envolvidos. Vamos à um exemplo prático de como efetuar tais operações.
4ª)Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos. Os extremos podem ser números reais como podem ser -\infty\, +\infty\
5ª){X € R / a < X < = b}
Escola de ensino fundamental e médio presindente geisel (polivalente)
Nomes:Ana Tandara de Melo Figueiredo
Kelry Andreza Ribeiro Pereira
Rafaely Cintia Rodrigues de Souza
1 ano "A"
1)Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
2)É uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais. Os números reais, podem ser também, resumidamente o conjunto de todos os números.
3)É a maneira mais fácil e intuitiva de realizar essas operações , através da representação gráfica dos intervalos envolvidos.
4)Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos. Os extremos podem ser números reais como podem ser -\infty\, e +\infty\,
5){xER/a < X < = b}
Polivalente -1ºa
Equipe: Anyelle de Oliveira
Valéria Medeiros
Valeska Medeiros
RESPOSTAS
1ª É importante porque é a representação gráfica dos conjuntos e sem ela não poderiamos entender o conjunto.
2ª É o conjunto universo, pois reuni todos os outros.
3ª Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos.
4ª É um número positivo infinito.
5ª{x E R | a < x < = b }
ESCOLA:POLIVATENTE 1°A
ALUNOS:Erica Rosangela
Roberta Diala
Sara Silva
1°Diagrama de Venn-Euler: é a representação gráfica dos conjuntos, através de entidades geométricas.
2°O Conjunto dos números reais é uma expansao do conjunto dos números racionais que emgloba nao só os inteiros e os fracionários,positivo e negativo,mas tambem todos os núme
ros irracionais.
3°Para poder representar os conjuntos, para que possomas indentificar e entender os conjunos com clareza.
4°Infinito positivo, para direita
5°{XER|A< X<=B}
1- é a representação gráfica dos conjuntos através de entidades geométricas.
2- incluem os números algébricas e os números transcendentais.O símbolo R usualmente representa este conjunto.
3- a importância é que contem cada número real entre dois extremos indicados, e possivelmente os proprios extremos.
4-infinito.
5-{X E R / A< X <=B}.
EQUIPE: MARIA IZABEL ALVES DO CARMO
TATIANA SAMPAIO SOUZA SÉRIE: 1ª ANO "A"
respostas:
1-é a representação gráfica dos conjuntos, através de entidades geométricas.
2-números reais é uma expansão do conjunto os números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais. Os números reais podem ser dispostos ordenadamente em uma reta que é chamada reta real.
3-Como intervalos são conjuntos é natural que as operações mencionadas possam ser realizadas. E, trata-se de um procedimento muito comum na resolução de alguns problemas.
4-representa infinito positivo.
5-S={xER/a< x < = b}
Escola:POLIVALENTE
alunas:MARIA YTELÂNIA ALVES CORREIA,MARIA AUXILIADORA GAMA DA SILVA e LUANA FELIX DE AQUINO.1ano"A"matutino
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XeR/ a< X < = b}
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XeR/a< X < =b}
1)A importância é que é uma forma gráfica de representar os conjuntos atravez de formas geográficas que o torna mais simples.
2)O conjunto dos números reais é a união de todo os conjuntos.
3)O intervalo são os subconjuntos do conjunto real que forma desigualdade ou números entre um e outro. O intervalo facilita o estudo e a solução dos conjuntos.
4)mais infinito (+∞)representa que a infinidade é crescente e é positiva.
5)S={X E R/a>X<=b}
Nomes: Rannael Adsson
Felipe Ferrucio
Jaelson Lima
Márcio Suellington
Serie: 1 ´´A``
Escola:Polivalente
Equipe:Amanda Almeida Silva, Cícera Ionara Rodrigues de Lima, Mayara Ferreira Melo da Silva
Turma:1º"A"
1ªEle é importante para a representação dos conjuntos.
2ªÉ representado pela letra R, é a união de todos os conjuntos. Ex[0,-1,4/3,0.5...]
3ªTrata-se de um procedimento muito comum na resolução de alguns procedimentos, é a maneira mais facil intuitiva de realizar essas operações é atravéz da representação gráfica dos intervalos envolvidos.
4ªSignifica um intervalo aberto de comprimento infinitivo.
5ª[X E R /a< X- =b]
EEFM POLIVALENTE
1º A
Thayna Pereira Brito
Damarys Yomara Ferreira
Natalia Maria de oliveira
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
Escola: E.E.F.M Polivalente Gaisel
Equipe: Bárbara Priscyla Silva de Sá
Cicera Karine Araujo Paulino
Maria Pâmela da Costa
Série: 1º "A"
Turno: Matutino
Professor: Ribamar Filho
Respostas:
1º- O Diagrama de Venn-Euler serve para calcular a representação gráfica dos conjuntos,atravez de entidades geométricas.
2º- É representado pela letra R,e é a união se todos os conjuntos.
3º- O Intervalo é o conjunto que contém cada número real entre dois extremos indicados,e possivelmente os próprios extremos.
4º- Representa o intervalo aberto de comprimento infinito positivo.
5º- {X E R / a< X-=b}
EEF POLIVALENTE
1°"D"
ILDERLANIO DE FREITAS
JOAO ELDYS ALVES BEZERRA
LYVIO FERREIRA MACHADO BESSA
1-Para facilitar o estudo sobre conjuntos.
2-É o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3-Para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4-Mais infinito,representa que a infinidade é crescente e positiva.
5-.s={XER / a < X < = b}
EEFM PRESIDENTE GEISEL"POLIVALENTE"
1 (D)
ILDERLANIO DE FREITAS PEDRO
LYVIO FERREIRA MACHADO BESSA
JOÃO EUDYS ALVES BEZERRA
1-para facilitar o estudo sobre conjuntos.
2-é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3-para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4-mais infinito,representa que a infinidade é crescente e positiva.
5-s={XER / a < X < = b}
respostas
1-para facilitar o estudo através de simbolos.
2-incluem os números algébricos e os números transcendentais .o simbolo R usualmente representa este conjunto.
3-um intervalo é um conjunto que contém cada número real entre dois extremos indicados , possivelmente os próprios extremos.
4-os números reais.
5-]a,b]={r e R :a < r < b}
nome : thiago fellipe
diogenes santos duarte
weslley santos
ítalo ferreira
EEFM POLIVALENTE
1ºD
ARYNE VANESSA VIEIRA SILVA
MARCOS JOSÉ BELO PAIVA
RODRIGO DA SILVA
1.é a representação gráfica dos conjuntos, através de entidades geométricas.
2.é o conjunto dos números transcedentes(números real)e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
EEFM POLIVALENTE
1ºD
ARYNE VANESSA VIEIRA SILVA
MARCOS JOSÉ BELO PAIVA
RODRIGO DA SILVA
1.é a representação gráfica dos conjuntos, através de entidades geométricas.
2.é o conjunto dos números transcedentes(números real)e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
EEFM POLIVALENTE
1ºD
kayck ferreira
walesson fernandes
jusceildo junior
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
Nayara Clementino Cunha
Ana Beatriz Bezerra
Carolina Paulo Silvestre de Pontes
1º D Manhã
1) A importância do Diagrama de Venn-Euler para a matematica é que através dele que podemos representar as entidades geométricas em forma de gráfico dos conjuntos.
2)O Numero reais são representado através do símbolo R
é usualmente represetados por números algébricos e os números transcendentais .
3) A importância é que diferencia o intervalo fechado e o intervalo aberto e é o conjunto dos números reais.
4)Intervalo fechado à esquerda de comprimento infinito.
5){x ε R |a ≤ x < b}
S(a,b)
EEFM POLIVALENTE
1º B
Manderson John de Lima Ferrreira
Weliton estrela rabelo
1.para facilitar o estudo sobre os conjuntos.
2.é o conjunto dos números transcedentes no qual o (número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
2°-R: IR, A UNIÃO ENTRE IN,ZL E Q E IRACIONAIS NÚMEROS E OPERAÇÕES SÃO ELAS: ADIÇÃO,SUBTRAÇÃO,MULTIPLICAÇÃO,DIVISÃO
E POTECIAÇÃO.
EEFM POLIVALENTE
1º B
Sarah Pereira Gomes
Rafael Gomes Pereira de Oliveira
1. Ele faz a representação gráfica dos conjuntos
2. É o conjunto de todos os números
3. Para indentificar os extremos que tanto podem ser infinitos ou reais
4. Que a infinidade é positiva
5. S = {XER / a < X < = b}
EEEFM POLIVALENTE
1º "B"
ANY KAROLINY DE LIMA PEREIRA
JAISA JANNIELLY RODRIGUES DA SILVA
THAMARA CAROLINE CARDOSO DE MELO
01-Para facilitar o estudo sobre conjunto
02-É o conjunto dos números transcendentes e dos números algébrico representado pela letra R
03-Para representar os conjuntos, para que possamos identificar e entender os conjuntos com mais clareza
04-Mais infinito, representa que a infinidade é crescente e positiva
05-s={XER / a < X < = b}
EEFM POLIVALENTE
1º B
Alef Ramalho
Árysson wandré
1- Ele ajuda na representação de Conjunto Assim como na união e Intersecção
2-
O conjunto dos números reais \mathbb{R}\, é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais. Os números reais, podem ser também, resumidamente o conjunto de todos os números.
3- Pra Nos Ajudar a definir o conjunto vendo se a bolinha é aberta ou fechada
4- mais infinito,representa que a infinidade é crescente e positiva.
5-s={XER / a < X < = b}
Equipe: Wallyson kelson, Amanda Pereira e Ana Kelly
Série: 1º "B" Data: 01/04/2009
Repostas:
1) Qual a importância do Diagrama de Venn-Euler para os conjuntos?
R: Para a versão booleana das quatros posições categoticas. Na qual não se faz uso da pressuposição existencial
2) Defina o conjunto dos números reais.
incluem os números algébricos e os números transcendentais. O símbolo{R} usualmente representa este conjunto.
3) Qual a importância do estudo do intervalo para solução de conjuntos ?
R: para descobrir o numero real entre dois extremos indicados e possivelmente os proprios extremos
4) o símbolo +∞ representa o que ?
R: significa um intervalo aberto ou fechado de um comprimento infinito
5) leia por extensão
{ x e R / a < x < b }
polivalente 1ano b
aluno:kelven elias freire
aluno:bruno bernardino de alcantara
respostas
1 é a representação gráfica dos conjuntos, através de entidades geométricas.
2 Conjuntos são um dos conceitos básicos da matemática.incluem os números algébricos e os números transcendentais.
3 Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos.
4 infinito positivo e para direita.
5 s={xer|a < x < b}
EEFM Presidente Geisel-Polivalente
1°"B"
Nome's:Rayan Pereira Silva
paulo Pereira Dos Santos
1-R:Para facilitar o estudo dos conjuntos.
2-R:São os numeros algebricos representados pela letra "R".
3-R:Para entendermos os conjuntos com mais claresa.
4-R:Que a infinidade é crescente e positiva.
5-R:s={XER / a < X < = b}
Jéssyka Thamyres e Ana Vanessa Lima . 1°"b"
1°-R:o diagrama de venn podem ser usado pr testar a validade de um silogismo
2°-R:IR a união entre IN,ZL,Q E IRACIONAIS
1) Qual a importância do Diagrama de Venn-Euler para os conjuntos?
R-E importante para melhor divisão dos cojuntos
2) Defina o conjunto dos números reais.
R-E definido pela letra (R) e pertece a os numeros algebricos
3) Qual a importância do estudo do intervalo para solução de conjuntos ?
R-E importante para intendermos com mas facilidade
4) o símbolo +∞ representa o que ?
R-Representa a infinidade dos numeros
5) Leia por extensão :
Representação de um intervalo na reta
S = {____________________}
R-s={XER / a < X < = b}
Alunos:yhrad thallison v.vieira
Christian allison batista candido
1ª ano (B)
EEFM POLIVALENTE
1º B
Nome josé andson ferreira do nascimento
Nome francisca wemelisa inacio de oliveira
1-É a importancia da represetacão gráficas dos conjuntos através de entidades geograficas.
2-É o conjunto dos números transcedentes[número real] e dos números algébricos representado pela letra r.
3-para representa mais os conjuntos, para que possamos identificar e entender os conjuntos.
4- representa que a infinidade é crescente e positiva.
5-s={x E r/a < x <= b}.
alunos: Amanda Pereira, Ana Kelly, Wallyson Kelson
1) a representação gráfica dos conjuntos, através de entidades geométricas.
2) uem os números algébricos e os números transcendentais. O símbolo \mathbb{R} usualmente representa este conjunto.
5) { X e R / a < X < = B}
Érica caroline renata wiliany wanessa
1.ano ''b''
1.Ele é importante por que é a representa ção gráfica dos conjuntos,através de entidades geométricas.
2.Números reais incluem os números algébricos e os números transcendentais. O símbolo {R} usualmente representa este conjunto.
3.O intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos.
4.Representa um conjunto que contém número real.
5.s={XER / a < X < = b}525
EEFM POLIVALENTE
1 ANO B
CINTHIA KATTIANE RODRIGUES DE MELO
SUYANE RODRIGUES DA SILVA
CICERA JANAINA DOS SANTOS
1-PAR FACILITA 0 ESTUDO DOS CONJUNTOS E A REPRESENTAÇÃO GRAFICA DOS CONJUNTOS ATRAVES DE ESTILIDADES GEOMÉTRICA.
2-EO CONJUNTO DOS NUMEROS TRANCEDENTES (NUMERO REAIS)E DOS NUMEROS ALGEBRICOS REPRESENTADO PELA SIGLA R .
3-SERVE PARA REPRESENTAÇÃO DOS CONJUNTOS PARA QUE POSSA INDENTIFICA COM CLARESA .
4-E UMA REPRESENTAÇÃO DE INFINIDADE E CRECENTE E PÓSITIVA
5- S={XER/A < X < B}
EEFM POLIVALENTE
1ºB
CICERO WALISSON
MARIA SOLANGE
1.Temos mais facilidade para resolvermos os conjuntos
2.O conjunto dos nùmeros reais são representados pele letra
(R).
3.Para que possamos endentificalosos os conjuntos
4.Mais indefinido e crescente positivo.
5.s= {XER/ a< X > =b}
EEFM POLIVALENTE
1º C
Nyelson Bruno Duarte
Emanoel Gomes Lima
Clara Ingrid Oliveira
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
Emaneol
EEFM POLIVALENTE
1ºC
JACKSON FERNANDES
JOSÉ ZEZON
JAILSON ALVES DE ARAÚJO
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
EEFM Polivalente
1º "C"
Ricardo Piancó De Lima
Maria Laleska Ferreira Soares
Maria Wyllma Lopes Bezerra
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
Polivalente
Cicera talita da silva
Ohanny rocha de freitas
1º 'C'
1ºPara facilitar o estudo dos conjuntos
2ºse define com os numeros algébricos e os numeros trancedentais
3º para entendermos com mais facilidade o estudo dos conjuntos
4º representa a infinidade positiva
5º {x E R |a < x < b }
Escola:Polivalente
Série:1º Ano "C"
Nome:Paloma Vitorino de B. Cavalcante
1.Para facilitar o conhecimento.
2.É consiste na junção de todos os outros conjuntos.
3.Os subconjuntos são chamados de intervalos.É importante porque facilita o estudo dos conjuntos.
4.Infinito.
5.x pertence aos reais tal que a menor que x
e b é maior ou menor que x.
1º c
rodrigo pianco de lima
erculis barreto alves
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b
ESCOLA POLIVALENTE
1º C
ALLYDIELSON SAMPAIO DE
NATALIA YSRAELLY BEZERRA DE SÁ
DÉBORA MAIARA DE SÁ BEZERRA
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
fernanda angra tavares marçal
magdala maxcimichaele da silva santos
serie: 1º"c"
data:01/04/2009
1.para facilitar o estudo sobre conjuntos.
2.se define com os numeros algébricos e os numeros transcedentes.
3.para entender os conjuntos com mais claresa
4.mais infinito, representa que a infinidade é crescente e positiva.
5.s={XER/a < X < = b}
EEFM POLIVALENTE
1º C
Marta Géssica Saraiva
1.para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
EEFM POLIVALENTE
1ºc
Izabelle Alves Duarte de Souza
ianne kelly de lima rodrigues
1.é a representação gráfica dos conjuntos, através de entidades geométricas.
2. incluem os números algébricos e os números transcendentais. O símbolo {R} usualmente representa este conjunto.
3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito.
5.s={X E R /a< X < =b}
EEFM POLIVALENTE
1ºC
NAYANE KELLY SILVA SAMPAIO
TATIANE PRICILA GOMES DE FREITAS
1.Facilita a representação dos conjuntos.
2.È o conjunto da união dos números racionais com os números irracionais,representado pela letra R.
3.Para entender os subconjuntos dos números reais que são determinados por desigualdades.
4.+infinitivo,quer dizer que a infinidade é crescente e positiva.
5.S={X E R / A < X <= B}
Luana Barbosa Lima 1ºc
Luana do Nascimento Alcantara 1ºc
1-E a representação grafica dos conjuntos,através das entidades geometricas.
2-defina-se dos números algébricos dos números transcendentais.
3-para entender os conjuntos com mais claresa.
4-Indica infinidade
5-{x E R:a < x < = b}
EEFM POLIVALENTE
1ºC
ELIZABETE DE OLIVEIRA LOPES
FLÁVIA TATIANE LOPES DA SILVA
1ºé a representação gráfica dos conjuntos, através de entidades geométricas
2°o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3ºpara representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4ºrepresenta o simbolo do infinito
5°s={XER / a < X < = b}
Polivelente
Bruno Daby Figerêdo de Souza-1ºC
Respostas
1.O diagrama de Venn representa de forma mais compreensível a união,a intersecção dos conjuntos,facilitando assim a aprendizagem e compreensão do aluno.
2.O conjunto dos números Reais engloba todos os outros conjuntos numéricos,ou seja,todos conjuntos numéricos são subconjunto dos Reais.
3.Na álgebra elementar, um intervalo é um conjunto que contém cada número real entre dois extremos indicados, e possivelmente os próprios extremos.
4.O infinito dos números positivo,ou seja,a infinidade crescente e positiva.
5.5.s={X E R / a < X ≤ b}
Nome:Gisele Mendonça Alencar
Série:1° ''C'' Manhã
Escola:Polivalente
1-para facilitar o estudo sobre conjuntos.
2-ntervalo real é um subconjunto dos números reais que não tem nenhum buraco. Ou seja, se I é um intervalo, a e b são elementos deste intervalo com a < b, entã3.para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.o todo número entre a e b também pertence ao intervalo.
3-possamos identificar e entender os conjuntos com mais claresa.
4-Representa a infinitividade se é crescente ou decrescente e positiva.
escola: polivalente
nome:alecxandra da silva braz
série:1º ano "c" turno:manhã
1-para ajudar no udos dos conjuntos
2-2-é uma coleção de objetos (chamados elementos). Os elementos podem representar qualquer coisa — números,
pessoas, letras, etc.
3-é importante já que o intrvalo digamos que está conectado aos conjuntos.
4-símbolo do infinito.
5-s={XER / a < X < = b}
polivalente
polivalente
nome;katiane lacerda da paz silva
nome;marise Daniele maciel lima
nome;juliana pereire de menezes
serie;1°(D)
1.O diagrama de venn é importante porque tem interseccao entre os conjontos onde pode ter uma relaçao entre eles em que algus elemento poder estar em dois conjuntos ao mesmo tempo.
O diagrama de Euler é importante para significa que ele é o seu subconjunto.
2.É o conjunto de todos os números algébricos transcedentes
3.É importante para aulgus subcojunto dos R que são determina dos por desigualdade.
4.Represeta o infinito
EEFM POLIVALENTE
1ºD
Amanda Máximo de Lima Miranda
Talicia Santana Soares
Nayara Silva Santos
1.Para auxiliar matemáticamente o estudo sobre conjuntos utilizando o diagrama.
2.O conjunto dos Numeros Reais é a expanção dos numeros racionais que engloba tambem todos os numeros irracionais.Os numeros reais podem ser tambem resumidamente o conjunto de todos os numeros.
3.A importância de entendermos com maior facilidade os conjuntos.
4.Mais finito,representando que ela é crescente e positiva.
5.s={XER/a<-x<=b}
EEFM POLIVALENTE
1ºD
Amanda Máximo de Lima Miranda
Talicia Santana Soares
Nayara Silva Santos
1.Para auxiliar matemáticamente o estudo sobre conjuntos utilizando o diagrama.
2.O conjunto dos Numeros Reais é a expanção dos numeros racionais que engloba tambem todos os numeros irracionais.Os numeros reais podem ser tambem resumidamente o conjunto de todos os numeros.
3.A importância de entendermos com maior facilidade os conjuntos.
4.Mais finito,representando que ela é crescente e positiva.
5.s={XER/a<-x<=b}
EEFM POLIVALENTE
1º'D'
Giovanna Nobre
Rebeca Filgueira
Francisco Natanael
1-É a representação gráfica dos conjuntos,através de entidades geométricas.
2-É uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários,positivos e negativos,mas também todos os números irracionais.
3-Para representar os conjuntos,para que possamos indentificar e entender os conjuntos com mais claresa.
4-Mais infinito,representa que a infinidade é crescente e positiva.
5-S={XER/a < x < = b}
EEFM POLIVALENTE
1°A
ROBERTA DIALA
ERIKA ROSANGELA
SARA SILVA
1.Para facilitar o estudo sobre conjuntos.
2.é o conjunto dos números algébricos representado pela letra R
3.Para representa os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4.mais infinito,representa que a infinidade é crescente e positiva.
5.s={XER / a < X < = b}
EEFM POLIVALENTE
1° 'C'
Nome: Jéssica Dayane
Jessyca Nayane
1 -> Para facilitar o estudo sobre conjuntos.
2 -> É o conjunto dos números transcedentes(número real) e dos números algébricos representado pela letra R.
3-> Para representar os conjuntos,para que possamos identificar e entender os conjuntos com mais claresa.
4-> Mais infinito,representa que a infinidade é crescente e positiva.
5->s={XER / a < X < = b}
1º) A forma mais usada é o que representa os elementos chamados ({}), a propriedade ou descrições de um conjunto são representados dentro de {} após os elementos representados deste por: e esclassivel de um diagrama devenn-euler: e a representação grafica do conjunto através de uma atitude geométrica.
2º)
a= { 2,3,5,7}
b= { 3,7,8,9}
3º) Na álgebra o elemento, um intervalo é um conjunto que contém cada nímero real entre 2 externos indicado, impossivelmente as propriedades externas. Os externos podem ser um número real, como podem ser ( -oo ) ( + oo ).
por exemplo: ]a.b[=(a,b)={xe IR:a +q x +q b }
4º) Representa a infinidade dos numeros naturais positivos.
5º) { x +q a -q b } .
Equipe: 1º "B"
Claudio da silva Araujo
Jheymison Silva de Oliveira
Gildeangleson oliveira de Araujo
Dupla:Gildeangleson oliveira de Araújo
Bruno Bernadino de Alcantara.
1ºano b Nº22 e 10
1ºA geometria é importante porque com ela aprendemos medidas e diametros e vários outros.
2ºEle foi um grande organizador da geometria.
3ºA palavra geometria é composta de duas palavras gregas: geos (terra) e metron (medida).Euclides é conhecido como Euclides de Alexandria, pois lá esteve para ensinar Matemática.
4º.As construções das pirâmides e templos pelas civilizações egípcia e Babilônica são o testemunho mais antigo de um conhecimento sistemático da Geometria
5ºQue depois da morte de Alexandre o grande ocorreram várias disputas entre generais do exercito em 306 a.c.
Postar um comentário