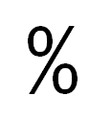PORCENTAGEM

Muitos acreditam que o símbolo "%" teria evoluído a partir da expressão matemática \frac x {100}.

Porém, alguns documentos antigos altamente sugerem que o % evoluiu a partir da escrita da expressão latina "per centum", sendo conhecido em seu formato atual desde meados do século XVII. Apesar do nome latino, a criação do conceito de representar valores em relação a uma centena é atribuída aos gregos.

Símbolo no século XV

Símbolo no século XVII

Símbolo a partir do século XVIII

Ponto percentual

Ponto Percentual é o nome da unidade na qual pode ser expressa o valor absoluto da diferença entre quaisquer pares de porcentagens.

Por exemplo: se uma determinada taxa de juros cair de 24% ao ano para 12% ao ano, pode-se dizer que houve redução de 50% {[(valor inicial)-(valor final)]/(valor inicial)} mas não que houve redução de 12%. Dizer que houve uma redução de 12% implica que o valor final seja de 12% menor que o valor inicial, no nosso exemplo, a taxa final seria 21,12% ao invés de 12%.

O Ponto Percentual é uma unidade que pode expressar essa diferença, voltando ao nosso exemplo, é correto dizer que houve redução de 12 pontos percentuais na tal taxa de juros.


Toda fração de denominador 100, representa uma porcentagem, como diz o próprio nome por cem.
Observe que o símbolo % que aparece nos exemplos acima significa por cento.
Se repararmos em nosso volta, vamos perceber que este símbolo % aparece com muita freqüência em jornais, revistas, televisão e anúncios de liquidação, etc.
Devemos lembrar que a porcentagem também pode ser representada na forma de números decimal

Trabalhando com Porcentagem
Vamos fazer alguns cálculos envolvendo porcentagens.
Exemplos:
1.Uma televisão custa 300 reais. Pagando à vista você ganha um desconto de 10%. Quanto pagarei se comprar esta televisão à vista?
2.Pedro usou 32% de um rolo de mangueira de 100m. Determine quantos metros de mangueira Pedro usou.
3.Comprei uma mercadoria por 2000 reais. Por quanto devo vende-la, se quero obter um lucro de 25% sobre o preço de custo.
4.Comprei um objeto por 20 000 reais e o vendi por 25 000 reais. Quantos por cento eu obtive de lucro?

Os números Irracionais

Os números irracionais são números que não se podem exprimir como uma razão (isto é, um quociente, uma fracção) de números inteiros. São… incalculáveis e incomensuráveis. Por isso também lhe chamaram números “mudos”, números“cegos”, números “surdos”, ou ainda números que “perderam a razão”…



A origem histórica da necessidade de criação dos números irracionais está ligada com dados de geométricos que se podem concretizar no problema da medida da diagonal do quadrado quando a comparada com o seu lado:


Teorema de Pitágoras:

" A soma dos quadrados dos catetos é igual ao quadrado da hipótenusa "



Dado um quadrado de lado igual à unidade,

quanto mede a diagonal?



Neste quadrado, de lado 1, verificamos que a diagonal d² = 1² + 1² = 2, então teremos que o comprimento da diagonal é dado pela √2.

Foi a tentar resolver este problema usando o Teorema de Pitágoras que os gregos descobriram um "novo" número: o número √2.

O Teorema de Pitágoras provocou, assim, a descoberta de novos números: os irracionais. Representam um marco importante para o pensamento humano, mas foi muito perturbadora para os pitagóricos. De tal maneira, que quiseram manter secreta esta descoberta.

A raiz quadrada de 2 é portanto um dos números irracionais mais célebres. Se tentarmos calculá-la vemos logo que deve ser 1 e …. Qualquer coisa. Mas a “qualquer coisa” é que é o problema! Alguns matemáticos antigos iam perdendo também a razão a tentar descobrir essa “qualquer coisa”! O mais que apuraram, pobres deles, foi 17/12, que é 1 mais “qualquer coisa” (1 é, como sabes, 12/12). Mas o quadrado de 17/12 é 289/144… E que 2 é… 288/144!

Era “quase”!

Os números irracionais são números que são quase exprimíveis como um quociente de números inteiros… Mas a que falta sempre o “quase”!

Assim,

Um número será irracional quando não se pode traduzir por uma fracção do tipo a/b. Dito de outra maneira: Um número diz-se irracional quando não pode exprimir-se por uma dízima finita ou infinita periódica. (Uma dízima será infinita periódica quando existir um conjunto de algarismos que se repete. Exemplo: 1,23452345... que muitas vezes se escreve 1,(2345). O período é o conjunto desses algarismos que se repetem, no nosso exemplo o período é 2345)



Curiosidade

O resultado d cálculo de √2 com algumas(250 ! ! !) casas decimais:
1.4142135623730950488016887242096980785696718753769480731766797 379907324784621070388503875343276415727350138462309122970249248 360558507372126441214970999358314132226659275055927557999505011 527820605714701095599716059702745345968620147285174186408891986 095523292304843087143214508397626036279952514079896872533965463...


Um irracional famoso

Talvez o mais famoso número irracional seja o PI ( ), o quociente entre o perímetro e o diâmetro de um círculo. As calculadoras científicas têm uma tecla para acesso directo a um valor aproximado de com dez, ou mais, dígitos. Por vezes, quando se calcula o perímetro ou uma área de um círculo utiliza‑se como valor aproximado de 3,14... mas actualmente ele já foi calculado com milhões de casas decimais

EXERCICIO:
1 - DE ACORROO COM OS NÚMEROS IRRACIONAIS PESQUISE SOBRE A ORIGEM DO SIMBOLO PI E PUBLIQUE EM SEU COMENTÁRIO !
2 - QUAL A PRINCIPAL DIFERENÇA ENTRE O CONJUNTO DOS NUMEROS RACIONAIS DO CONJUNTO DOS NUMEROS IRRACIONAIS!
3 - IDENTIFIQUE AS PRINCIPAIS PREMISSAS DO TEXTO ACIMA !

Aula 01 02 03 04 Matemática

Lógica matemática

Lógica Matemática é o uso da lógica formal para estudar o raciocínio matemático-- ou, como propõe Alonzo Church (*Introduction to Mathematical Logic* (Princeton, New Jersey: Princeton University Press, 1956; décima edição, 1996), 'lógica tratada pelo método matemático'. No início do século XX, lógicos e filósofos tentaram provar que a matemática, ou parte da matemática, poderia ser reduzida à lógica.(Gottlob Frege, p.ex., tentou reduzir a aritmética à lógica; Bertrand Russell e A. N. Whitehead, tentaram reduzir toda a matemática então conhecida à lógica -- a chamada 'lógica de segunda ordem'.) Uma das suas doutrinas lógico-semânticas era que a descoberta da forma lógica de uma frase, na verdade, revela a forma adequada de dizê-la, ou revela alguma essência previamente escondida. Há um certo consenso que a redução falhou -- ou que precisaria de ajustes --, assim como há um certo consenso que a lógica -- ou alguma lógica -- é uma maneira precisa de representar o raciocínio matemático. Ciência que tem por objeto o estudo dos métodos e princípios que permitem distinguir raciocínios válidos de outros não válidos.

Sudoku é um jogo de raciocínio e lógica. Apesar de ser bastante simples, é divertido e viciante. Basta completar cada linha, coluna e quadrado 3x3 com números de 1 a 9. Não há nenhum tipo de matemática envolvida.

Exercício !!
Resolver o Sudoku acima !!! em folha e entregar até dia 11-05 - 2009 (trabalho de dupla ) .